RMQ问题&ST表 浅析

什么是RMQ问题？

RMQ(Range Min/Max Query):

对于长度为n的数组A，回答若干询问RMQ(A,i,j)(i,j<=n-1)返回数组A中下标在i,j范围内的最小（大）值，即RMQ问题是指求区间最值的问题。

解决方式：

• 朴素算法：每查询一次为O(n)
• ST算法：高效，以O(n log n)的预处理代价，换取O(1)的查询时性能

ST算法

令：f[i,j]代表从第i个数起连续2^j个数中的最大值（因此要用倍增）

从下图可以看出：f[0][1]=max(f[0][0],f[1][0]), …… f[[0][2]=max(f[0][1],f[2][1]) ……

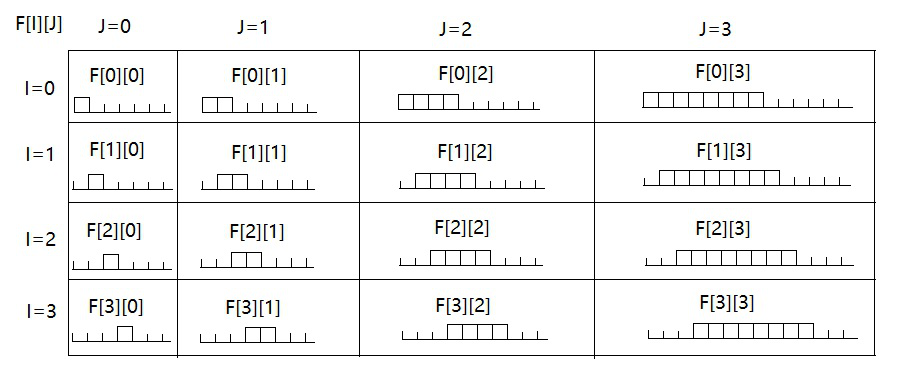
采用动态规划的思想：显然f[i,j]=max(f[i,j-1],f[i+2^(j-1),j-1])

所以，我们需要建立ST表，也就是上文中的f数组。生成ST表是一次预处理，此后都是O(1)的查询了。

建立ST表

for(int i=0; i<=n; i++) f[i][0]=a[i]; //初始化，第0列(j=0)就是a[i]。
for(int j=1; j<=20; j++)  //j<20很大啦，够用！2^20=1048576
	for(int i=0; i+(1<<j)<=n+1; i++)
		f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);

查询时，只需取在ST表中找2段头尾满足区间范围进行拼凑，有重叠覆盖不影响结果。

Why?我们来模拟一下：

设A=2，6，4，8，4，8，4，8
求RMQ(A,0,5)[MAX值]=max(RMQ(A,0,3),RMQ(A,2,5))，无论是直接求还是分两段重复的区间求的结果都是8
因为不是运算，所以有重叠部分是可以的哦！

查询

设：范围是 [m,n] ,这个范围不会是刚好2 ^k的长度，我们就用2段区间来拼凑：

即[m,m+2^k-1]和[n-2^k+1,n] (拼凑后头尾满足[m,n],中间允许重叠)

因此查询结果即为：RMQ[A,m,n]=max(f[m][k],f[n-(1<<k)+1][k]);

其中2^k<=(n-m+1) 则 k=log2(n-m+1);

举个例子：查询RMQ[A,1,6]=max(f[1][2],f[3][2])

log对数函数

这里的log来说一下，对数是对求幂的逆运算，正如除法是乘法的倒数

如果a^x =N（a>0，且a≠1），那么数x叫做以a为底N的对数，记作x=loga N，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。

比如说2^5=32，log2 32=5，求的是n次方

ST表例题

【模板】ST表-Luogu

#include<bits/stdc++.h>
using namespace std;
const int maxn=2000001;
int n,m,a[maxn],lg[maxn],f[maxn][25];
int main()
{
    scanf("%d%d",&n,&m);
    //读入&预处理
    for(int i=1; i<=n; i++){
        scanf("%d",&a[i]);
        f[i][0]=a[i];
    }
    for(int j=1; j<=20; j++)
        for(int i=1; i+(1<<j)<=n+1;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    //回答每个询问
    for(int i=1; i<=m; i++){
        int l,r; scanf("%d%d",&l,&r);
        int k=log2(r-l+1),ans=max(f[l][k],f[r-(1<<k)+1][k]); //直接使用cmath头文件里的`log2`函数
        printf("%d\n",ans);
    }
    return 0;
}

质量检测-Luogu

//裸的模版题，只不过是没有询问需要自己“手动添加”罢了
//还有一个点就是题目中求的是min值就要将原模版中的所有max改成min才能pass哦
#include<bits/stdc++.h>
using namespace std;
const int N=1000000+10;
int f[N][25],n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++) scanf("%d",&f[i][0]);
    for(int k=1; k<=20; k++)
    	for(int i=1; i<=n; i++)
    		if(i+(1<<k)-1<=n) f[i][k]=min(f[i][k-1],f[i+(1<<(k-1))][k-1]);
    for(int i=1; i<=n-m+1; i++){
        int s=log2(m);
        printf("%d\n",min(f[i][s],f[i+m-(1<<s)][s]));
    }
    return 0;
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议